El astrónomo holandés Jan Hendrik Oort fue el primero en descubrir el problema de la «materia perdida» en los años 1930. Observando los valores de red-shift (desplazamiento hacia el rojo) de estrellas que se mueven cerca del plano de nuestra galaxia, Oort supuso que podía calcular cómo de rápido se movían dichas estrellas. Puesto que la galaxia se mantiene unida, razonó que debía haber suficiente materia dentro de la galaxia de modo que la fuerza gravitacional central fuese lo bastante fuerte como para que las estrellas no escaparan, al igual que la atracción gravitacional del Sol mantiene un planeta en su órbita. Pero ocurrió que cuando realizó el cálculo, se dió cuenta de que no había suficiente materia en la galaxia.

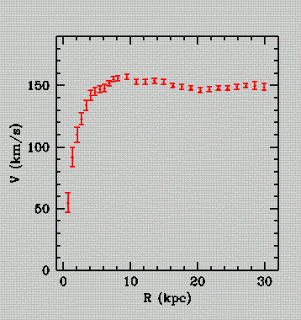
La discrepancia no era pequeña: la galaxia debería ser al menos 2 veces tan masiva como la suma de las masas de todas sus componentes visibles. ¿Dónde estaba entonces toda esa materia oculta? Además, en los 1960, se obtuvieron medidas del perfil de la velocidad tangencial de las estrellas en sus órbitas, como función de su distancia al centro de la galaxia. Se encontró que una vez que nos alejamos del centro de la galaxia, todas las estrellas se mueven a la misma velocidad, independientemente de su distancia al centro galáctico (ver la figura siguiente). Normalmente, como en el caso de nuestro sistema solar, cuanto mas alejado está un objeto, más despacio viaja en su órbita.

Un gran problema cosmológico

Para poder visualizar la seriedad del problema cosmológico al que nos enfrentamos, necesitamos considerar solo un poco la dinámica Newtoniana.

• Para cambiar el vector velocidad de un cuerpo –bien en dirección , bien en magnitud, o ambas– debe aplicarse una fuerza a la masa del cuerpo. La aceleración resultante será igual al cociente entre la fuerza aplicada y la masa del objeto, es decir, f = m.a, donde f es la fuerza aplicada al cuerpo, m es la masa del cuerpo y a es la aceleración resultante (cambio de la velocidad). Tanto f como a son vectores; el cambio en la dirección de la velocidad se producirá en la dirección de la fuerza aplicada.
• Cuando un atleta olímpico se dispone a lanzar el martillo, lo mueve alrededor de él en círculos. La fuerza que siente en sus brazos (la fuerza que está aplicando al martillo) es la «fuerza centrípeta». Esa fuerza es igual al producto de la masa del martillo, m, multiplicada por la aceleración centrípeta (la cual es, en este caso, la aceleración que cambia continuamente la dirección, no la magnitud, del vector velocidad del martillo (en dirección hacia el atleta, tal para mantenerlo en una órbita circular alrededor del atleta). Esta aceleración es igual al cuadrado de la velocidad tangencial del martillo, v, dividida por el radio R del círculo. Así, la fuerza «hacia adentro» que necesita ejercer el atleta para mantener el martillo en su órbita circular es: f = m.v²/R.
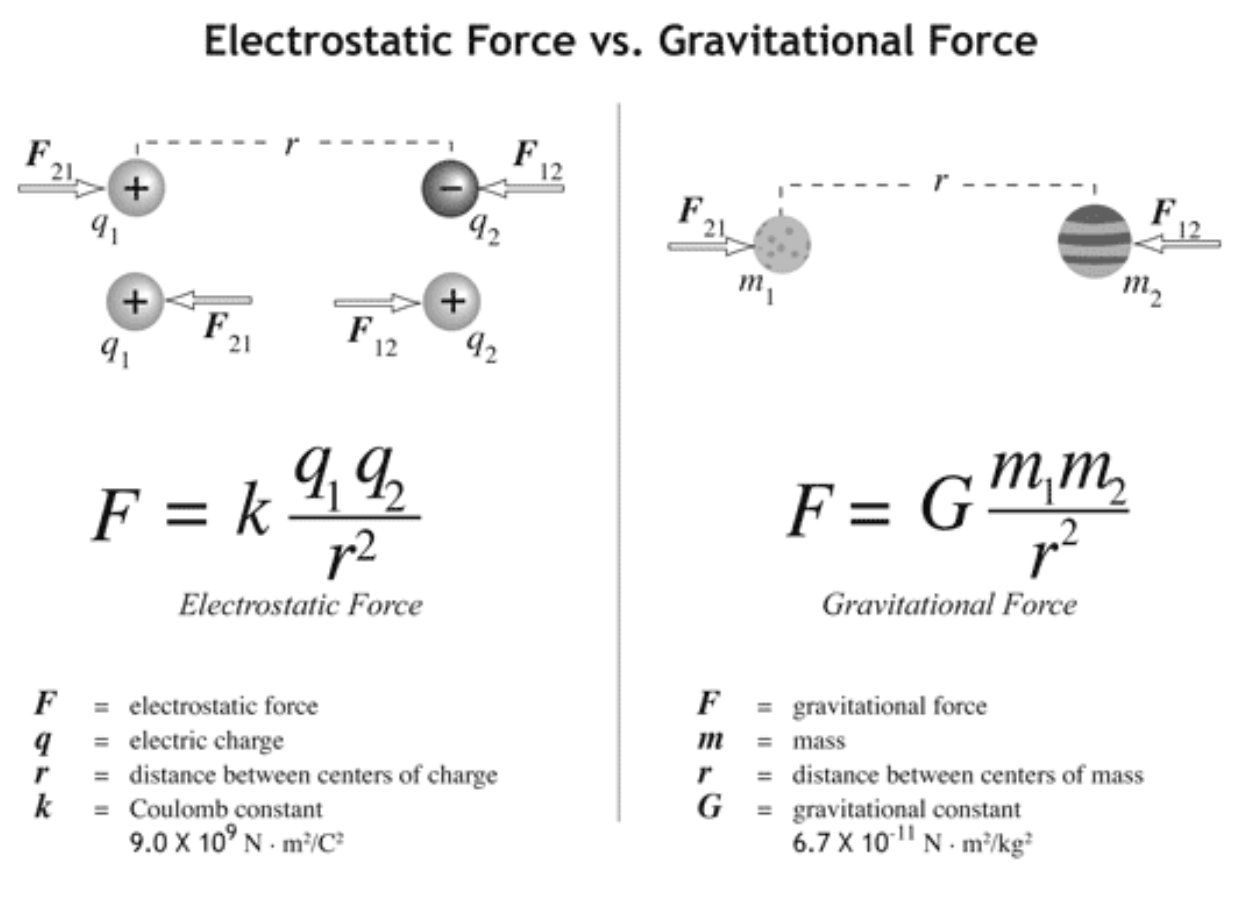
• La ley de la gravitación de Newton nos dice que la fuerza entre dos masas es igual a G (la ‘constante’ de gravitación universal) multiplicada por el producto de las dos masas y dividido por el cuadrado de la distancia entre ellas F = G.(m1 x m2)/R².

Consideremos el caso de una estrella en los confines de la galaxia. Su radio, desde el centro de la galaxia, es R. Su masa es m1, y m2 es la masa total de todo lo demás (todas las demás estrellas y la materia) contenida en un círculo cuyo radio es R, la distancia de la estrella al centro de la galaxia. La dinámica Newtoniana asume que toda la masa combinada, m2, actúa como si dicha masa estuviera localizada en un punto en el centro de la galaxia. Para que la estrella se mantenga en una órbita fija, la fuerza centrípeta (hacia el interior) necesaria, m1.V²/R, debe ser igual exactamente a la fuerza (gravitacional) disponible, G.(m1 x m2)/R². Igualando estas dos expresiones obtenemos la expresión m2 = (V²).R / G

Salvemos a Newton añadiendo más masa

La fórmula anterior nos dice que para que la velocidad tangencial de la estrella, V, se mantenga constante conforme R aumenta, tal como nos indica el gráfico de arriba, la masa incluida total, m2, debería incrementarse proporcionalmente al radio R. Pero nos damos cuenta que, si nos alejamos del centro, hacia las pocas últimas estrellas en cualquier galaxia, la masa incluida no aumenta proporcionalmente al radio. Así pues, parece ser que no hay forma de que la velocidad pueda mantenerse constante para las estrellas más exteriores, como ocurre con las interiores.

Entonces, los astrofísicos han concluido que, o bien existe masa «perdida» en las regiones exteriores de la galaxia, o bien las estrellas más alejadas que rotan alrededor del núcleo de la galaxia no obedecen a la ley de la Gravitación Universal de Newton. Lo segundo es impensable para la astrofísica clásica newtoniana de hoy en día, por lo tanto es necesario añadir masa de alguna manera. Postulemos entonces que existe una masa que no vemos. La llamaremos «materia oscura» porque no sabemos lo que es. Ha pasado casi un siglo y la Astrofísica sigue sumida en la oscuridad.

Existen problemas también a mucha mayor escala. En 1933 el astrónomo Fritz Zwicky anunció que cuando midió las velocidades individuales de un gran grupo de galaxias, conocido como el cluster de la Coma, encontró que todas las galaxias que había medido estaban moviéndose tan rápidamente las unas respecto a las otras que el cluster debería deshacerse. La masa visible de las galaxias que conforman el cluster era demasiado pequeña para producir la suficiente fuerza gravitacional para mantener unido el cluster. Así, que no solo es nuestra galaxia la que tiene menos masa de la esperada, sino que también ocurre con un cluster entero de galaxias.

¿Era necesario inventarse más masa?

La Cosmología del Plasma (o Física del Plasma) nos dice que NO. Estamos hablando de una ciencia física actual de estudio en muchas universidades y laboratorios del mundo, que se fundamenta en la existencia y actividad del plasma eléctrico. 

El plasma (eléctrico) se considera el cuarto estado fundamental de la materia. Un detalle trascendental: el plasma está presente en el 99,9% de Universo, algo que no ocurre con la materia. Sabemos también que la fuerza eléctrica actúa en todas las escalas, desde la infinitesimal hasta la más global. Otro dato importante: la fuerza eléctrica es 39 órdenes de magnitud mayor que la fuerza gravitatoria.

La Física del Plasma ha avanzado mucho en los últimos años, ayudada por una propiedad importante de la fuerza eléctrica: su adaptabilidad («escalabilidad»). Esto quiere decir que cualquier fenómeno eléctrico observado a gran escala (Universo) es reproducible a pequeña escala (laboratorio). La Electrodinámica del plasma, a nivel galáctico, soporta perfectamente los fenómenos observados como por ejemplo el problema tratado aquí.  Es más, mediante métodos computacionales y también reproducidos en condiciones de ingravidez, el plasma eléctrico es capaz de reconfigurarse en morfologías espirales. Evidentemente la fuerza gravitatoria existe. El problema es despreciar el efecto cosmológico de la fuerza eléctrica.